Sejarah, Definisi dan Cara Kerja Algoritma Divide and Conquer.
Sejarah Algoritma Devide dan Conquer
Awal dari algoritma ini utamanya adalah pengurangan dan penaklukan - masalah asli secara berturut-turut dipecah menjadi sub-masalah tunggal, dan memang dapat diselesaikan secara berulang.
Pencarian biner, algoritma penurunan-dan-taklukkan di mana sub-masalah berukuran kira-kira setengah dari ukuran aslinya, memiliki sejarah yang panjang. Sementara deskripsi yang jelas tentang algoritma pada komputer muncul pada tahun 1946 dalam sebuah artikel oleh John Mauchly, gagasan untuk menggunakan daftar item yang diurutkan untuk memfasilitasi pencarian tanggal kembali setidaknya sejauh Babylonia pada 200 SM.
Algoritma penurunan-dan-taklukkan kuno lainnya adalah algoritma Euclidean untuk menghitung pembagi persekutuan terbesar dari dua bilangan dengan mengurangi bilangan tersebut menjadi subproblem ekuivalen yang lebih kecil dan lebih kecil, yang berasal dari beberapa abad SM.
Contoh awal dari algoritma bagi-dan-taklukkan dengan beberapa subproblem adalah deskripsi Gauss tahun 1805 tentang apa yang sekarang disebut algoritma Cooley – Tukey fast Fourier transform (FFT), meskipun dia tidak menganalisis jumlah operasinya secara kuantitatif, dan FFT tidak tersebar luas sampai mereka ditemukan kembali lebih dari satu abad kemudian.
Algoritma D&C dua sub problem awal yang secara khusus dikembangkan untuk komputer dan dianalisis dengan benar adalah algoritma pengurutan gabungan, yang ditemukan oleh John von Neumann pada tahun 1945.
Contoh penting lainnya adalah algoritma yang ditemukan oleh Anatolii A. Karatsuba pada tahun 1960 [8] yang dapat mengalikan dua angka n-digit di O (n log 2 3) {\ displaystyle O (n ^ {\ log _ {2} 3} )} O (n ^ {\ log _ {2} 3}) operasi (dalam notasi Big O). algoritma ini menyangkal dugaan Andrey Kolmogorov tahun 1956 bahwa operasi Ω (n 2) {\ displaystyle \ Omega (n ^ {2})} \ Omega (n ^ {2}) diperlukan untuk tugas tersebut.
Definisi Algoritma Devide dan Conquer
Dalam ilmu komputer, Algoritma divide and conquer adalah paradigma desain algoritma yang didasarkan pada rekursi multi-cabang. Algoritme bagi-dan-taklukkan bekerja dengan memecah masalah secara rekursif menjadi dua atau lebih sub-masalah dari jenis yang sama atau terkait, hingga masalah ini menjadi cukup sederhana untuk diselesaikan secara langsung.
Cara Kerja Algoritma Devide dan Conquer
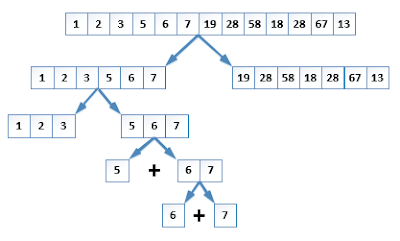
Contoh sederhana : Misalkan, untuk menghitung total jumlah dari bilangan-bilangan yang ada di dalam sebuah list, kita dapat menggunakan perulangan sederhana
nums = [1, 2, 3, 5, 6, 7, 19, 28, 58, 18, 28, 67, 13]
total = 0
for i in range(0, len(nums)):
total = total + nums[i]
print(total) # 255Algoritma perulangan yang digunakan pada kode di atas memang sederhana dan memberikan hasil yang benar, tetapi terdapat beberapa masalah pada kode tersebut, yaitu perhitungan dilakukan secara linear, yang menghasilkan kompleksitas O(n). Hal ini tentunya cukup ideal untuk ukuran list kecil, tetapi jika ukuran list menjadi besar (beberapa Milyar elemen) maka perhitungan akan menjadi sangat lambat. Kenapa perhitungannya menjadi lambat? Karena nilai dari total tergantung kepada kalkulasi nilai total sebelumnya. Kita tidak dapat melakukan perhitungan total dari depan dan belakang list sekaligus, sehingga kita dapat mempercepat perhitungan dua kali lipat. Dengan kode di atas, kita tidak dapat membagi-bagikan pekerjaan ke banyak pekerja / CPU!
Lalu apa yang dapat kita lakukan? Langkah pertama yang dapat kita lakukan adalah menerapkan teknik rekursif untuk membagi-bagikan masalah menjadi masalah yang lebih kecil. Jika awalnya kita harus menghitung total keseluruhan list satu per satu, sekarang kita dapat melakukan perhitungan dengan memecah-mecah list terlebih dahulu:
def sums(lst):
if len(lst) >= 1:
return lst[0]
mid = len(lst) // 2
left = sums(lst[:mid])
right = sums(lst[mid:])
return left + right
print(sums(nums)) # 255 Apa yang kita lakukan pada kode di atas?
- Baris if len(lst) >= 1 memberikan syarat pemberhentian fungsi rekursif, yang akan mengembalikan isi dari list ketika list berukuran 1 (hanya memiliki satu elemen).
- Baris mid = len(lst) // 2 mengambil median dari list, sebagai referensi ketika kita membagi list menjadi dua bagian.
- Baris left = sum(lst[:mid]) dan selanjutnya membagikan list menjadi dua bagian, dengan nilai mid sebagai tengah dari list.
Singkatnya, setelah membagikan list menjadi dua bagian terus menerus sampai bagian terkecilnya, kita menjumlahkan kedua nilai list tersebut, seperti pada gambar berikut:


Tidak ada komentar:
Posting Komentar